Bài toán tháp Hà Nội – Thuật toán và cách giải

Bởi

Tháp Hà Nội là một trong những bài toán kinh điển của giới lập trình. Hầu như bất kể ai mới học lập trình, đặc biệt là môn cấu trúc dữ liệu và giải thuật đều có nghe nói hoặc đã từng phải giải bài toán này.

💦 Đọc thêm về thuật toán:

Bài viết hôm nay, chúng ta sẽ cùng nhau tìm hiểu bài toán tháp Hà Nội là gì? Thuật toán để giải bài toán tháp Hà Nội.

Nội dung chính của bài viết

Bài toán tháp Hà Nội (The Tower of Hanoi)
Thuật toán để giải bài toán tháp Hà Nội
Code Java giải bài toán tháp Hà Nội

Bài toán tháp Hà Nội (The Tower of Hanoi)

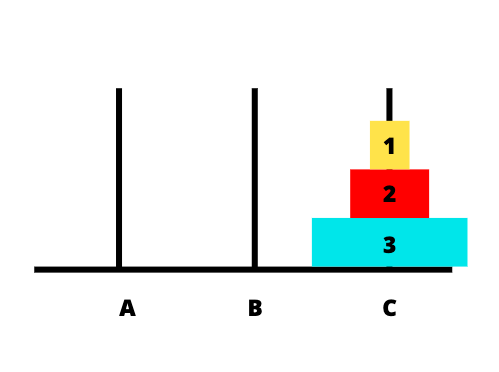
Bài toàn tháp Hà Nội là trò chơi toán học gồm 3 cọc và n đĩa có kích thước khác nhau. Ban đầu các đĩa được xếp chồng lên nhau trong cọc A như hình vẽ.

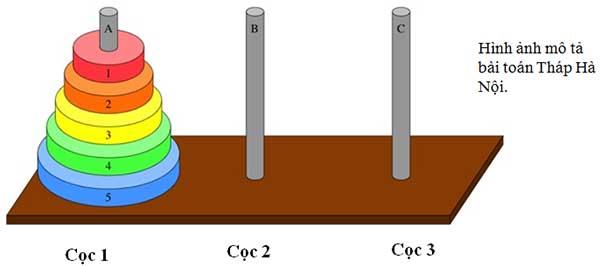
Yêu cầu của bài toán: Di chuyển toàn bộ các đĩa ở cọc A sang cọc C với điều kiện sau.

Mỗi lần thực hiện chỉ được di chuyển một đĩa
Các đĩa phải xếp theo nguyên tắc, đĩa lớn ở dưới, đĩa nhỏ ở trên.
Được phép thêm một cọc B làm trung gian để di chuyển các đĩa.

Ngoài lề: Mặc dù có tên quốc tế là tháp Hà Nội nhưng lại được phát minh bởi nhà toán học người Pháp Édouard Lucas từ thế kỷ 19. Nó gắn liền với truyền thuyết về ngôi đền Hindu, nơi người ta cho rằng câu đố được sử dụng để tăng tính kỷ luật tinh thần cho các linh mục trẻ.

Thuật toán để giải bài toán tháp Hà Nội

Để dễ hình dung hơn các bước giải, chúng ta sẽ lấy ví dụ cụ thể. Giả sử chúng ta có 3 cọc A, B, C tương trưng cho 3 tháp và có 3 đĩa.

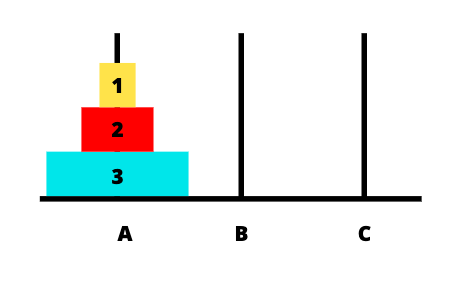
Để giải quyết bài toán này, giải pháp đơn giản nhất là sử dụng đệ quy. Để đưa toàn bộ 3 đĩa ở cọc A tới cọc C, bạn cần:

Chuyển đĩa 1 và 2 sang cọc trung gian B.
Di chuyển đĩa 3 sang cọc C
Chuyển đĩa 1 và 2 sang cọc C

Tất nhiên, chúng ta không thể làm điều này một cách thủ công. Chúng ta sẽ tạo một hàm đệ quy để làm điều đó.

Hình dưới đây mô tả chi tiết các bước khi thực hiện:

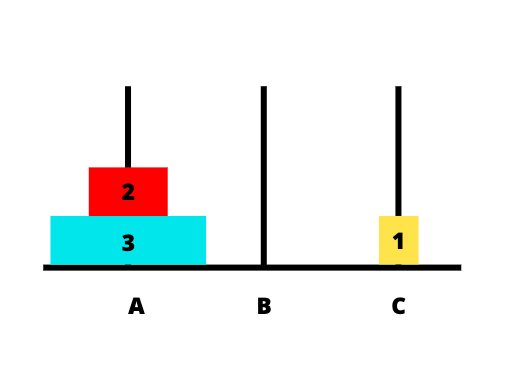
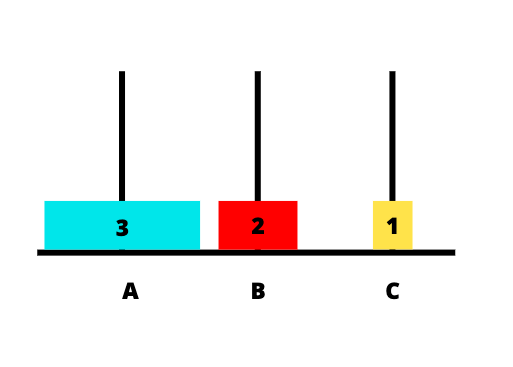
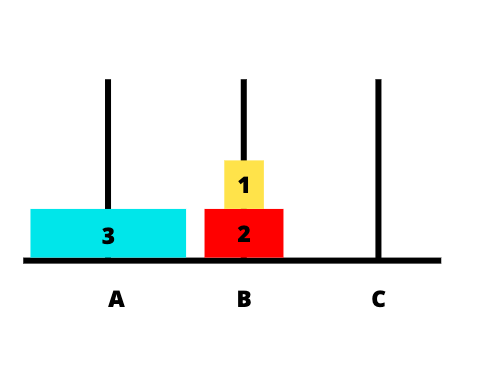
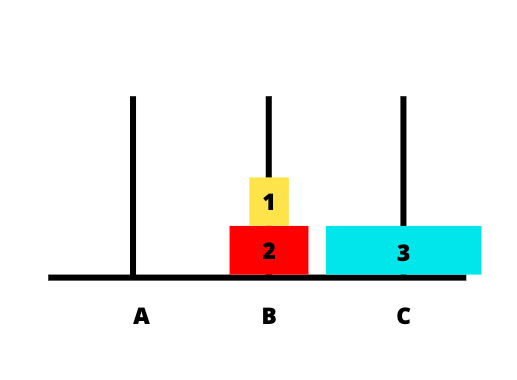
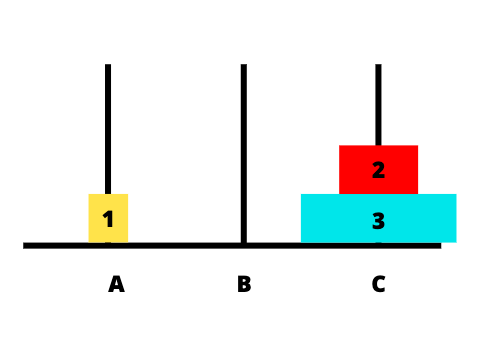
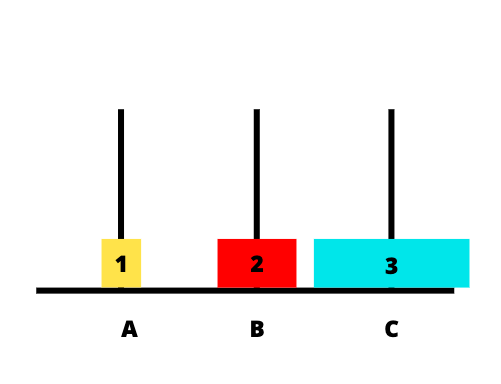
Tháp Hà Nội (Tower of Hanoi) — Trạng thái bắt đầu

Tower of Hanoi — Di chuyển đĩa 1 từ cọc A sang cọc C

Code Java giải bài toán tháp Hà Nội

Sau khi đã hiểu rõ tư tưởng thuật toán để giải bài toán tháp Hà Nội. Chúng ta sẽ cùng nhau viết code để implement giải pháp bằng lập trình.

Trong code, chúng ta sẽ chia là 2 phần: base case và phần gọi đệ quy.

1. Base case

Base case của chúng ta sẽ giải quyết với trường hợp số đĩa n = 1

if (n == 1) {
    System.out.println("Take disk 1 from rod " +  from_rod + " to rod " + to_rod);
    return;
}

2. Gọi đệ quy

Bằng cách gọi đệ quy, chúng ta sẽ giải quyết được bài toán tháp Hà Nội với n > 1.

towerOfHanoi(n-1, from_rod, helper_rod, to_rod);
       System.out.println("Take disk " + n + " from rod " +  from_rod + " to rod " + to_rod);
       towerOfHanoi(n-1, helper_rod, to_rod, from_rod);
}

Mình giải thích chi tiết hơn một chút, cách gọi trên sẽ tương đương:

Di chuyển toàn bộ (n-1) đĩa trên cùng sang cọc trung gian (cọc B)
Di chuyển đĩa còn lại ở cọc A sang cọc C
Di chuyển (n-1) từ cọc trung gian B ngược trở lại cọc C.

Code java đầy đủ:

public class Main {
    static void towerOfHanoi(int n, char from_rod, char to_rod, char helper_rod)
    {
        if (n == 1)
        {
            System.out.println("Take disk 1 from rod " +  from_rod + " to rod " + to_rod);
            return;
        }
        towerOfHanoi(n-1, from_rod, helper_rod, to_rod);
        System.out.println("Take disk " + n + " from rod " +  from_rod + " to rod " + to_rod);
        towerOfHanoi(n-1, helper_rod, to_rod, from_rod);
    }
 
    public static void main(String args[])
    {
        int n = 5;
        towerOfHanoi(n,'A','C', 'B');
    }
 
}

Bài toán tháp Hà Nội với n đĩa thì cần ít nhất (2^n – 1) bước thực hiện di chuyển đĩa. Ví dụ, nếu có 3 đĩa thì số bước di chuyển đĩa ít nhất là (2^3-1) = 7 bước.