Thuật Toán Đồ Thị với JavaScript: Tìm Kiếm Theo Chiều Rộng và Chiều Sâu

Trong thế giới phát triển phần mềm, thuật toán đồ thị là một công cụ cực kỳ mạnh mẽ giúp chúng ta xử lý và giải quyết các bài toán liên quan đến dữ liệu có mối quan hệ. Một trong những phương pháp phổ biến nhất khi làm việc với đồ thị chính là các thuật toán Tìm Kiếm Theo Chiều Rộng (BFS) và Tìm Kiếm Theo Chiều Sâu (DFS). Nhưng tại sao chúng lại quan trọng và làm sao để bạn có thể sử dụng chúng với JavaScript?

Vì Sao Thuật Toán Đồ Thị Quan Trọng?

Đồ thị là một cách tuyệt vời để biểu diễn nhiều loại cấu trúc dữ liệu phức tạp. Bạn có thể tưởng tượng một mạng xã hội, nơi mỗi người dùng là một “đỉnh” (node) và mỗi mối quan hệ bạn bè giữa hai người dùng là một “cạnh” (edge). Đó là một ví dụ điển hình của đồ thị. Đồ thị còn được sử dụng trong nhiều lĩnh vực khác như:

• Điều hướng GPS: Biểu diễn đường đi giữa các địa điểm.
• Khoa học máy tính: Biểu diễn cây phân cấp thư mục hoặc các hệ thống tập tin.
• Phân tích mạng xã hội: Giúp chúng ta hiểu cách người dùng tương tác với nhau.

Với việc hiểu được thuật toán đồ thị, bạn có thể giải quyết nhiều bài toán phức tạp như tìm đường đi ngắn nhất, xác định các nhóm liên quan, và nhiều hơn thế nữa.

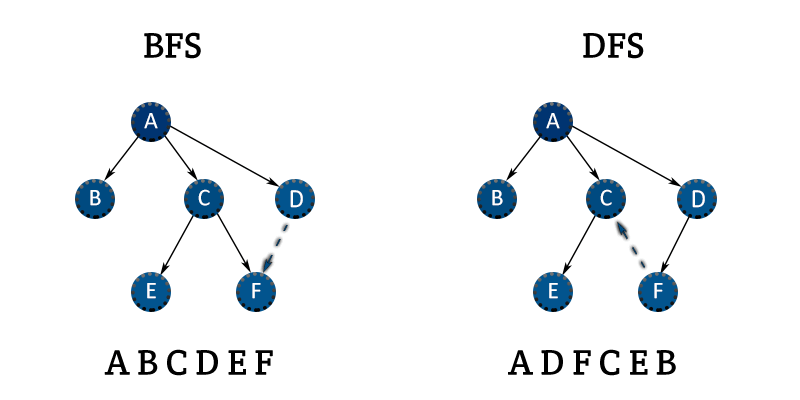
Tìm Kiếm Theo Chiều Rộng (BFS) và Tìm Kiếm Theo Chiều Sâu (DFS) Là Gì?

Cả BFS và DFS đều là các phương pháp duyệt qua đồ thị, nhưng chúng có cách tiếp cận rất khác nhau. Hãy cùng tìm hiểu từng thuật toán một cách chi tiết!

Tìm Kiếm Theo Chiều Rộng (Breadth-First Search – BFS)

BFS là thuật toán bắt đầu từ một đỉnh (node) ban đầu, sau đó duyệt qua tất cả các đỉnh kế cận trước khi chuyển sang cấp tiếp theo. Bạn có thể tưởng tượng nó giống như bạn đi qua từng tầng một của một tòa nhà, khám phá toàn bộ các phòng trên một tầng trước khi chuyển sang tầng kế tiếp.

Cách Hoạt Động:

1. Khởi tạo: Bắt đầu từ một đỉnh và thêm nó vào một hàng đợi (queue).
2. Duyệt qua các đỉnh kế cận: Lần lượt lấy từng đỉnh từ hàng đợi, kiểm tra các đỉnh kế cận của nó và thêm chúng vào hàng đợi.
3. Lặp lại: Lặp lại quá trình này cho đến khi không còn đỉnh nào trong hàng đợi.

function bfs(graph, startNode) {
  let queue = [startNode];
  let visited = new Set();
  visited.add(startNode);

  while (queue.length > 0) {
    const currentNode = queue.shift();
    console.log(currentNode); // In ra đỉnh hiện tại

    graph[currentNode].forEach(neighbor => {
      if (!visited.has(neighbor)) {
        visited.add(neighbor);
        queue.push(neighbor);
      }
    });
  }
}

// Đồ thị dạng đối tượng
const graph = {
  'A': ['B', 'C'],
  'B': ['D', 'E'],
  'C': ['F'],
  'D': [],
  'E': ['F'],
  'F': []
};

bfs(graph, 'A'); // Kết quả: A, B, C, D, E, F

Tìm Kiếm Theo Chiều Sâu (Depth-First Search – DFS)

DFS thì ngược lại, nó đi sâu vào từng nhánh của đồ thị trước khi quay lại. Hãy tưởng tượng bạn đi vào một mê cung, bạn sẽ đi đến cuối ngõ cụt trước khi quay trở lại để khám phá các đường khác.

Cách Hoạt Động:

1. Khởi tạo: Bắt đầu từ một đỉnh và thêm nó vào một ngăn xếp (stack).
2. Duyệt qua các đỉnh kế cận: Lấy đỉnh từ đỉnh ngăn xếp và tiếp tục đi sâu vào các đỉnh kế cận của nó cho đến khi không còn đỉnh nào có thể đi tiếp.
3. Lặp lại: Lặp lại quá trình cho đến khi tất cả các đỉnh đã được duyệt qua.

function dfs(graph, startNode) {
  let stack = [startNode];
  let visited = new Set();
  visited.add(startNode);

  while (stack.length > 0) {
    const currentNode = stack.pop();
    console.log(currentNode); // In ra đỉnh hiện tại

    graph[currentNode].forEach(neighbor => {
      if (!visited.has(neighbor)) {
        visited.add(neighbor);
        stack.push(neighbor);
      }
    });
  }
}

// Đồ thị dạng đối tượng
const graph = {
  'A': ['B', 'C'],
  'B': ['D', 'E'],
  'C': ['F'],
  'D': [],
  'E': ['F'],
  'F': []
};

dfs(graph, 'A'); // Kết quả: A, C, F, B, E, D

So Sánh BFS và DFS

BFS:

• Ưu điểm: Tìm được đường đi ngắn nhất trong đồ thị không trọng số.
• Nhược điểm: Sử dụng nhiều bộ nhớ hơn so với DFS khi xử lý các đồ thị lớn.

DFS:

• Ưu điểm: Sử dụng ít bộ nhớ hơn BFS, dễ dàng triển khai bằng đệ quy.
• Nhược điểm: Không đảm bảo tìm được đường đi ngắn nhất.

Cả BFS và DFS đều có ứng dụng rộng rãi trong các bài toán đồ thị, và mỗi thuật toán có thế mạnh riêng của nó tùy vào yêu cầu của từng bài toán cụ thể.

Ứng Dụng Thực Tế Của BFS và DFS

1. Tìm Đường Trong Mê Cung

Nếu bạn muốn tìm đường ra trong một mê cung, BFS sẽ giúp bạn tìm được con đường ngắn nhất. Trong khi đó, DFS có thể giúp bạn khám phá mọi ngóc ngách của mê cung, tuy nhiên có thể không hiệu quả bằng.

2. Phân Tích Mạng Xã Hội

Bạn có thể sử dụng BFS để tìm mối quan hệ giữa hai người dùng trong một mạng xã hội, ví dụ tìm người quen chung.

3. Tìm Kiếm Trên Web

Công cụ tìm kiếm sử dụng DFS để duyệt qua các trang web. Nó đi sâu vào từng liên kết để tìm nội dung liên quan trước khi quay trở lại.

Kết Luận

Qua bài viết này, chúng ta đã cùng tìm hiểu hai thuật toán tìm kiếm quan trọng trong đồ thị là BFS và DFS. Mỗi thuật toán có ưu và nhược điểm riêng, và việc chọn lựa đúng thuật toán sẽ giúp bạn giải quyết bài toán của mình hiệu quả hơn. Hãy thử áp dụng chúng vào các bài toán thực tế của mình, từ việc giải đố mê cung đến việc tìm kiếm trong mạng xã hội!

Nếu bạn đang tìm hiểu thêm về lập trình đồ thị và muốn tìm hiểu sâu hơn về cách áp dụng chúng trong các dự án thực tế, hãy tham khảo thêm tài liệu và các bài viết khác tại VNTALKING. Chúng tôi luôn sẵn sàng chia sẻ kiến thức và kinh nghiệm lập trình để giúp bạn phát triển sự nghiệp của mình!

​Miễn phí khóa học React Native

Bạn có muốn download toàn bộ video của khóa học rất nổi tiếng về React Native này không? Đăng kí để mình gửi link download nhé

DOWNLOAD