Chắc hẳn ai từng theo học ngành công nghệ thông tin đều từng ngán ngẩm môn “cấu trúc dữ liệu và giải thuật“. Không biết mọi người thế nào, chứ bản thân mình thì môn này trượt lên trượt xuống.
Rồi thời gian trôi nhanh như pet chạy ngoài đồng. Nhìn lại cũng đã đi làm được vài năm, cũng phải va vấp vào thuật toán. Đúng là ghét của nào trời trao của ấy.
Có bạn nào đi phỏng vấn mà bị nhà tuyển dụng hỏi về thuật toán không? Chắc là có đúng không!
Hầu như ai làm về phần mềm thì đều phải làm việc với thuật toán. Bất kể phần mềm lớn hay nhỏ thì đều phải vận dụng thuật toán.
Bài viết này, mình sẽ tổng hợp 5 thuật toán phổ biến nhất mà mọi lập trình viên nên biết.
Cùng bắt đầu nhé.
Nội dung chính của bài viết
5 thuật toán phổ biến nhất
Để các bạn dễ theo dõi, mình sẽ sắp xếp theo mức độ phổ biến của thuật toán.
1. Thuật toán sắp xếp nhanh (Quick Sort)
Thuật toán Quick Sort được phát triển bởi C.A.R
Đúng như tên gọi, thuật toán sắp xếp nhanh là một thuật toán cho kết qua nhanh, gọn, nhẹ. Thuật toán này dựa trên việc chia một mảng thành các mảng nhỏ hơn.
Nếu so với các thuật toán sắp xếp khác như Insertion Sort hay sắp xếp nổi bọt (Bubble Sort), thì thuật toán sắp xếp nhanh cho tốc độ nhanh hơn đáng kể.
Thuật toán Quick sort là một thuật toán chia để trị (divide and Conquer Algorithm). Nó sẽ chọn một phần tử trong mảng làm điểm đánh dấu (pivot). Sau khi lựa chọn được điểm pivot, bước tiếp theo sẽ chia mảng thành nhiều mảng con dựa vào pivot đã chọn. Và lặp đi lặp lại như vậy cho đến khi kết thúc.
Tốc độ của thuật toán bị ảnh hưởng bởi việc chọn pivot. Có nhiều cách chọn pivot, dưới đây là một số cách:
- Luôn chọn phần tử đầu tiên của mảng làm pivot.
- Luôn chọn phần tử cuối cùng của mảng.
- Chọn ngẫu nhiên 1 phần tử trong mảng.
- Chọn phần tử có giá trị nằm giữa mảng (median element).
Để mình họa cho thuật toán sắp xếp nhanh, chúng ta cùng thực hành một bài toán: Sắp xếp mảng sau theo thứ tự tăng dần: [10, 7, 8, 9, 1, 5]
Quicksort example program in c++:
#include<iostream>
#include<cstdlib>
using namespace std;
// Swapping two values.
void swap(int *a, int *b)
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}
// Partitioning the array on the basis of values at high as pivot value.
int Partition(int a[], int low, int high)
{
int pivot, index, i;
index = low;
pivot = high;
// Getting index of the pivot.
for(i=low; i < high; i++)
{
if(a[i] < a[pivot])
{
swap(&a[i], &a[index]);
index++;
}
}
// Swapping value at high and at the index obtained.
swap(&a[pivot], &a[index]);
return index;
}
// Random selection of pivot.
int RandomPivotPartition(int a[], int low, int high)
{
int pvt, n, temp;
n = rand();
// Randomizing the pivot value in the given subpart of array.
pvt = low + n%(high-low+1);
// Swapping pivot value from high, so pivot value will be taken as a pivot while partitioning.
swap(&a[high], &a[pvt]);
return Partition(a, low, high);
}
int QuickSort(int a[], int low, int high)
{
int pindex;
if(low < high)
{
// Partitioning array using randomized pivot.
pindex = RandomPivotPartition(a, low, high);
// Recursively implementing QuickSort.
QuickSort(a, low, pindex-1);
QuickSort(a, pindex+1, high);
}
return 0;
}
int main()
{
int n, i;
cout<<"\nEnter the number of data elements to be sorted: ";
cin>>n;
int arr[n];
for(i = 0; i < n; i++)
{
cout<<"Enter element "<<i+1<<": ";
cin>>arr[i];
}
QuickSort(arr, 0, n-1);
// Printing the sorted data.
cout<<"\nSorted Data ";
for (i = 0; i < n; i++)
cout<<"->"<<arr[i];
return 0;
}
2. Thuật toán sắp xếp nổi bọt (Bubble Sort)
Thuật toán sắp xếp nổi bọt (Bubble Sort) là thuật toán sắp xếp một mảng số bằng cách đổi chỗ 2 số liên tiếp nhau nếu chúng đứng sai thứ tự (số sau bé hơn số trước với trường hợp sắp xếp tăng dần) cho đến khi không thể đổi chỗ được nữa.
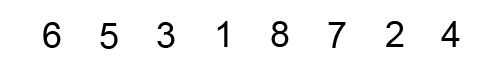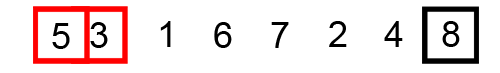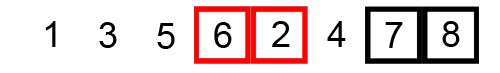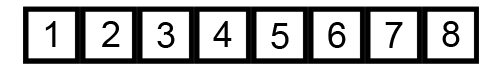
Việc sắp xếp có thể tiến hành từ trên xuống hoặc từ dưới lên.
Ví dụ minh họa: sắp xếp dãy số [5 1 4 2 8] tăng dần.
#include <stdio.h>
void swap(int &x, int &y)
{
int temp = x;
x = y;
y = temp;
}
// Hàm sắp xếp bubble sort
void bubbleSort(int arr[], int n)
{
int i, j;
bool haveSwap = false;
for (i = 0; i < n-1; i++){
// i phần tử cuối cùng đã được sắp xếp
haveSwap = false;
for (j = 0; j < n-i-1; j++){
if (arr[j] > arr[j+1]){
swap(arr[j], arr[j+1]);
haveSwap = true; // Kiểm tra lần lặp này có swap không
}
}
// Nếu không có swap nào được thực hiện => mảng đã sắp xếp. Không cần lặp thêm
if(haveSwap == false){
break;
}
}
}
/* Hàm xuất mảng */
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf("n");
}
// Driver program to test above functions
int main()
{
int arr[] = {5 1 4 2 8};
int n = sizeof(arr)/sizeof(arr[0]);
bubbleSort(arr, n);
printf("Dãy số tăng dần: n");
printArray(arr, n);
return 0;
}
3. Thuật toán tìm kiếm nhị phân (Binary search)
Thuật toán Tìm kiếm nhị phân (Binary Search) là một thuật toán cao cấp hơn tìm kiếm tuần tự.
Đối với các dãy số lớn, thuật toán này tốt hơn hẳn so với các thuật toán tìm kiếm khác. Nhưng nó đòi hỏi dãy số phải được sắp xếp từ trước.
Tuy thuật toán binary search có ưu điểm là tìm kiếm nhanh, nhưng cũng có nhược điểm là nếu danh sách bị thay đổi, danh sách đó phải được sắp xếp lại trước khi tiến hành tìm kiếm tiếp. Và thao tác này thường tốn thời gian.
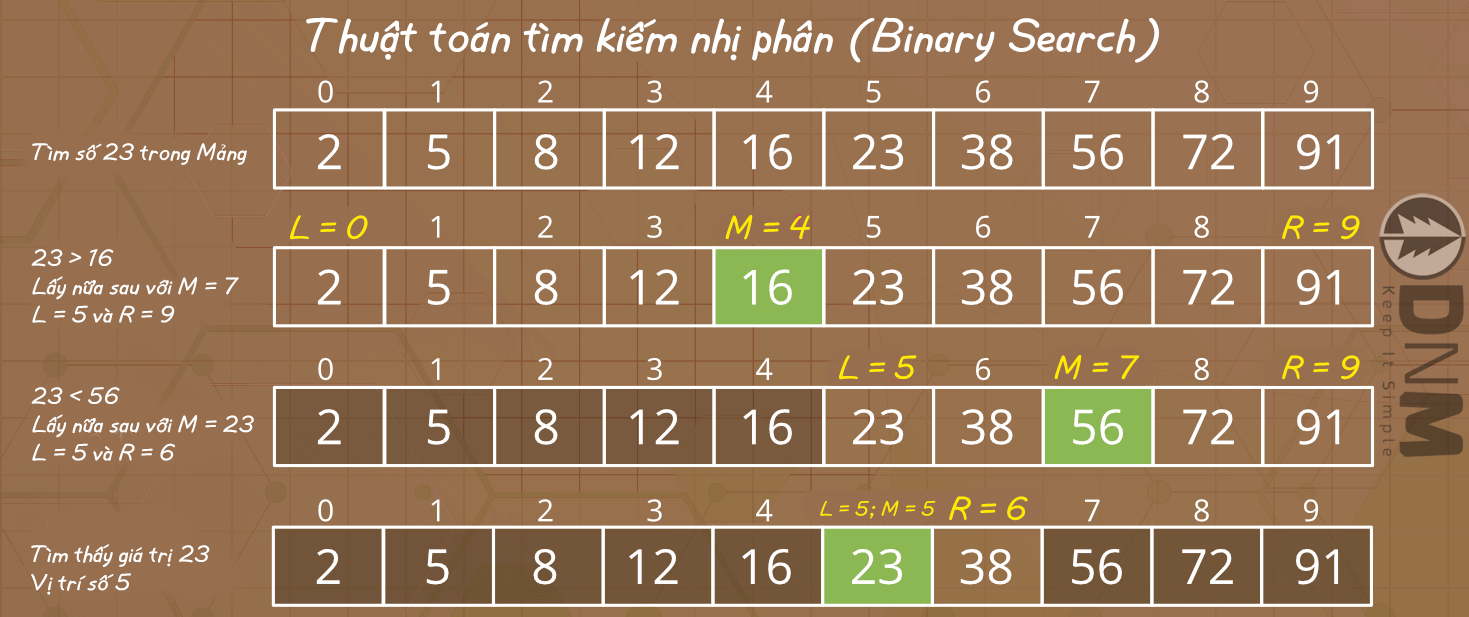
Minh họa cho thuật toán tìm kiếm nhị phân, chúng ta cùng làm bài toán sau: Tìm vị trí phần tử có giá trị là 23 trong một mảng A[2,5,8,12,16,23,38,56,72,91] đã được sắp xếp.
#include <iostream>
using namespace std;
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
if (r >= l) {
int mid = l + (r - l) / 2;
// If the element is present at the middle
// itself
if (arr[mid] == x)
return mid;
// If element is smaller than mid, then
// it can only be present in left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Else the element can only be present
// in right subarray
return binarySearch(arr, mid + 1, r, x);
}
// We reach here when element is not
// present in array
return -1;
}
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int n = sizeof(arr) / sizeof(arr[0]);
int result = binarySearch(arr, 0, n - 1, x);
(result == -1) ? cout << "Element is not present in array"
: cout << "Element is present at index " << result;
return 0;
}
4. Thuật toán Dijkstra – tìm đường đi ngắn nhất
Với bài toán tìm đường đi ngắn nhất, chúng ta có một số thuật toán nổi tiếng giải quyết nó như: Dijkstra hay Floyd.
Thuật toán Dijkstra có 2 loại là
- Tìm đường đi ngắn nhất từ 1 đỉnh nguồn tới 1 đỉnh đích.
- Tìm đường đi ngắn nhất từ 1 đỉnh nguồn tới các đỉnh còn lại của đồ thị.
Dưới đây là code minh họa cho loại thứ 1 của thuật toán Dijkstra.
void Dijkstra(void)
/*Đầu vào G=(V, E) với n đỉnh có ma trận trọng sốA[u,v]≥0; s∈V */
/*Đầu ra là khoảng cách nhỏ nhất từ s đến các đỉnh còn lại d[v]: v∈V*/
/*Truoc[v] ghi lại đỉnh trước v trong đường đi ngắn nhất từ s đến v*/
{
/* Bước 1: Khởi tạo nhãn tạm thời cho các đỉnh*/
for (v∈V) {
d[v] = A[s, v];
truoc[v] = s;
}
d[s] = 0; T = V\{s}; /*T là tập đỉnh có nhãn tạm thời*/
/* Bước lặp */
while (T != φ) {
#Tìm đỉnh u∈T sao cho d[u] = min{ d[z] | z∈T };
T = T\{u}; /*cố định nhãn đỉnh u*/;
For(v∈T) { /* Gán lại nhãn cho các đỉnh trong T*/
If(d[v] > d[u] + A[u, v]) {
d[v] = d[u] + A[u, v];
truoc[v] = u;
}
}
}
}
5. Hashing
Hashing là một thuật toán giúp phân biệt giữa các khối dữ liệu với nhau. Ứng dụng nổi bật và quan trọng nhất của thuật toán này đó chính là cho phép tìm kiếm và tra cứu một bản ghi dữ liệu đã cho trước và mã hóa bản ghi đó một cách nhanh chóng.
Thuật toán này cho phép phát hiện và sửa lỗi khi dữ liệu bị làm nhiễu bởi các quá trình ngẫu nhiên.
Ngoài ra, thuật toán này cũng có thể sử dụng cho phép tạo ra các giá trị dữ liệu không trùng lặp (Unique) và ứng dụng trong các bộ định tuyến để lưu trữ địa chỉ IP.
Tạm kết
Như vậy là mình đã tổng kết 5 thuật toán phổ biến nhất, hay “bị hỏi nhất” khi đi phỏng vấn xin việc.
Nếu bạn muốn tìm hiểu thêm về thuật toán thì nên tìm cuốn “cấu trúc dữ liệu và giải thuật”. Đây chính là cuốn gối đầu giường cho người muốn học kỹ về thuật toán.
Mình hi vọng, bài viết này sẽ hữu ích cho bạn. Mình không cần gì chỉ cần một lần share của bạn thôi 🙂



















Bình luận. Cùng nhau thảo luận nhé!