Level Order Traversal là gì? Hãy cùng mình thảo luận về nó trong bài viết này nhé! Ngoài ra, mình sẽ in từng cấp độ của tree và mình sẽ sử dụng hai cách tiếp cận chính là Recursive (Đệ quy) và Iterative để xem sự khác biệt về độ phức tạp giữa chúng là gì.
Ok, bắt đầu thôi nào.
Nội dung chính của bài viết
Level Order Traversal
Level Order Traversal còn được gọi là Breadth First Traversal (duyệt cây theo chiều rộng) vì nó đi qua tất cả các node ở mỗi cấp độ trước khi chuyển sang cấp độ tiếp theo (độ sâu).
Hãy xem hình minh họa dưới đây để thấy rõ các cấp độ của một Binary Tree:
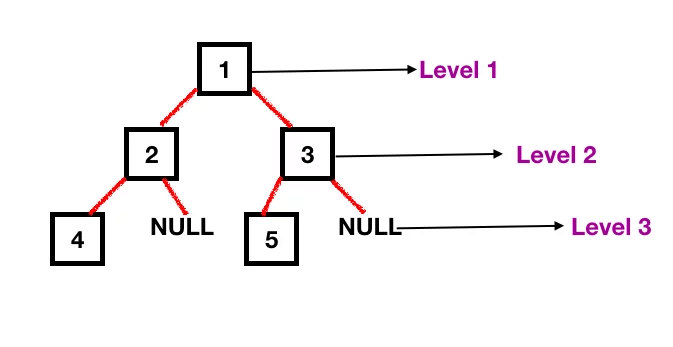
– Cấp độ cuối cùng của cây luôn bằng với chiều cao của cây.
– Cấp cuối cùng của cây phải chứa ít nhất một node.
Tiếp theo, dưới đây là lớp định nghĩa cấu trúc dữ liệu của Binary Tree.
public class BinaryTree {
public TreeNode root;
public static class TreeNode {
public TreeNode left;
public TreeNode right;
public Object data;
public TreeNode(Object data) {
this.data = data;
left = right = null;
}
}
}
Sau khi bạn đã hiểu rõ hơn về Binary Tree, hãy cùng mình viết chương trình Java bằng các phương pháp tiếp cận Iterative và Recursive cho Breadth First Traversal.
Breadth First Traversal – Đệ quy
Dưới đây là chương trình Java sử dụng cách tiếp cận Recursive để in từng cấp độ của tree:
package com.journaldev.tree.levelOrderTraversal;
import com.journaldev.tree.height.BinaryTree;
import com.journaldev.tree.height.BinaryTree.TreeNode;
public class PrintLevelsOfTree {
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
/**
* Binary Tree in our example, height = 2
* 1 (Root)
* 2 3 (Level 1)
* 4 5 (Level 2)
*/
binaryTree.root = new BinaryTree.TreeNode(1);
binaryTree.root.left = new BinaryTree.TreeNode(2);
binaryTree.root.right = new BinaryTree.TreeNode(3);
binaryTree.root.left.left = new BinaryTree.TreeNode(4);
binaryTree.root.right.left = new BinaryTree.TreeNode(5);
printLevelsRecursively(binaryTree.root);
}
private static void printLevelsRecursively(TreeNode root) {
int height = heightOfTree(root);
for (int i = 1; i <= height; i++) {
System.out.print("Level " + i + " : ");
printSingleLevelRecursively(root, i);
System.out.println();
}
}
private static int heightOfTree(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = heightOfTree(root.left);
int rightHeight = heightOfTree(root.right);
return Math.max(leftHeight, rightHeight) + 1;
}
private static void printSingleLevelRecursively(TreeNode root, int level) {
if (root == null)
return;
if (level == 1) {
System.out.print(root.data + " ");
} else if (level > 1) {
printSingleLevelRecursively(root.left, level - 1);
printSingleLevelRecursively(root.right, level - 1);
}
}
}
Kết quả output được in ra là:
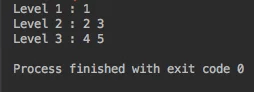
– Độ phức tạp thời gian – O(n^2)
– Độ phức tạp không gian – O(1)
Để giảm thiểu độ phức tạp đó, bạn hãy tối ưu hóa chương trình trên bằng cách sử dụng phương pháp Iterative.
public static void printLevelsIteratively(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode node = queue.peek();
if (node != null) {
System.out.print(node.data + " ");
queue.remove();
if (node.left != null)
queue.add(node.left);
if (node.right != null)
queue.add(node.right);
}
}
}
Kết quả của phương pháp này sẽ được in ra như sau:
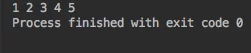
Trong đoạn mã trên, mỗi node được xếp hàng một lần.
– Độ phức tạp thời gian – O (n)
– Độ phức tạp không gian – O (n)
Kích thước của Queue bằng số lượng node.
Vì vậy trong cách tiếp cận ở trên, mình đã chuyển đổi một số space để tối ưu hóa cách tiếp cận.
Bài hướng dẫn này của mình kết thúc ở đây. Mong rằng những thông tin này sẽ giúp bạn viết chương trình Java một cách tối ưu nhất. Chúc bạn có một ngày làm việc vui vẻ và tràn đầy năng lượng. Best regards!
😉 Đọc các bài viết khác về thuật toán:
















![[Dự đoán] 3 xu hướng phát triển ứng dụng mobile HOT nhất 2023 Xu hướng phát triển ứng dụng Android](https://vntalking.com/wp-content/uploads/2018/11/xu-huong-phat-trien-ung-dung-android-80x60.png)







Bình luận. Cùng nhau thảo luận nhé!