Dijkstra là một trong những thuật toán rất nổi tiếng trong giới lập trình. Nghe tới những bài toán liên quan tới tìm đường đi ngắn nhất là nghĩ ngay tới thuật toán Dijkstra.
Dijkstra là thuật toán được đặt tên theo nhà khoa học máy tính người Phần Lan, người đã phát minh ra nó. Thuật toán này nhằm mục đích tìm đường đi ngắn nhất trong đồ thị có cạnh với trọng số dương.
Nội dung chính của bài viết
Tổng quan thuật toán Dijkstra
Trước khi đi vào chi tiết nội dung thuật toán, chúng ta cần phải hiểu những thuật ngữ sau:
- Graph (đồ thị): Đồ thị là một cấu trúc dữ liệu phi tuyến tính được định nghĩa là G = (V, E), trong V là tập hợp hữu hạn các đỉnh (node), E là tập hợp hữu hạn các cạnh, cạnh là một đường nối giữa hai node với nhau.
- Weighted graph (đồ thị có trọng số): Tương tự như đồ thị ở trên, chỉ khác là mỗi cạnh sẽ được gán thêm một trọng số. Kiểu như cùng một khoảng cách đi từ A đến B, nhưng đi đường đẹp thì nhanh hơn, đường làng nhiều ổ gà thì chậm hơn.
- Connected graph (đồ thị liên thông): Một đồ thị được gọi là liên thông (connected) nếu có đường đi giữa mọi cặp đỉnh phân biệt của đồ thị. Ngược lại, đồ thị này được gọi là không liên thông
- Spanning tree (cây khung): một spanning tree của đồ thị G là cây con của đồ thị G, chứa tất cả các đỉnh của G. Nói cách khác, cây bao trùm của một đồ thị G là một đồ thị con của G, chứa tất cả các đỉnh của G, liên thông và không có chu trình. Cây bao trùm của đồ thị liên thông G cũng có thể định nghĩa như một đồ thị con không chu trình lớn nhất, hay một đồ thị con liên thông nhỏ nhất của G
Thuật toán Dijkstra giải quyết bài toán gì?
Cho một đồ thị có trọng số (đặt tên là đồ thị G). Mục tiêu là tìm đường đi ngắn nhất từ một đỉnh cho trước đến các đỉnh còn lại của đồ thị G.
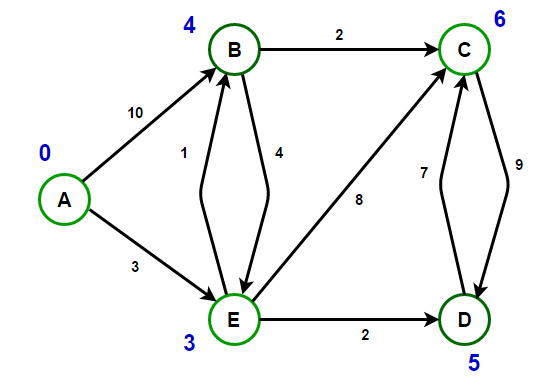
Đồ thị G có các đặc điểm sau:
- Gồm tập hợp các đỉnh (V)
- Tập hợp các cạnh (E). Trong đó ký hiệu (q,r) là biểu diễn một cạnh nối giữa hai đỉnh q và r, cost(q,r) thì biểu thị trọng số của cạnh đó.
Ý tưởng thực hiện thuật toán Dijkstra
Thuật toán Dijkstra dựa trên nguyên tắc giảm bớt. Trong đó các giá trị chính xác hơn sẽ dần thay thế một giá trị gần đúng với khoảng cách chính xác cho đến khi đạt được khoảng cách ngắn nhất. Khoảng cách gần đúng tới mỗi định được ước tính lớn hơn nhiều khoảng cách thực và sẽ dần thay thế bằng giá trị nhỏ nhất của giá trị cũ bằng độ dài của một đường mới tìm được.
Thuật toán sử dụng hàng đợi ưu tiên kết hợp với thuật toán tham lam chọn đỉnh gần nhất chưa được xử lý và thực hiện quá trị giảm bớt này trên tất cả các cạnh mà nó duyệt qua.
Giả thuật các bước thực hiện:
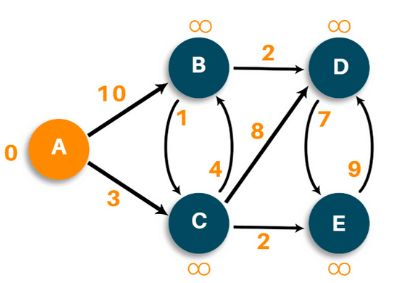
Bước 1: Đánh dấu tất các node dự kiến: Đặt khoảng cách từ nút nguồn tới nút 0 là nguồn, và đặt là vô hạn với các nút khác.
Bước 2: Tiến hành chạy lặp (loop):
- Trích xuất nút N là nút có khoảng cách nhỏ nhất
- Thêm liên kết tới nút N vào cây đường đi ngắn nhất
- Sau đó tiến hành tối ưu các đường đi cạnh N bằng cách thử kéo dài cạnh
Mã nguồn c++ minh họa thuật toán tìm đường đi ngắn nhất
Thuật toán có thể được implement bởi bất kỳ ngôn ngữ nào: C++, Java, hay Python…
Dưới đây là code minh họa bằng C++
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
// Data structure to store a graph edge
struct Edge {
int source, dest, weight;
};
// Data structure to store a heap node
struct Node {
int vertex, weight;
};
// A class to represent a graph object
class Graph
{
public:
// a vector of vectors of `Edge` to represent an adjacency list
vector<vector<Edge>> adjList;
// Graph Constructor
Graph(vector<Edge> const &edges, int n)
{
// resize the vector to hold `n` elements of type vector<Edge>
adjList.resize(n);
// add edges to the directed graph
for (Edge const &edge: edges)
{
// insert at the end
adjList[edge.source].push_back(edge);
}
}
};
void printPath(vector<int> const &prev, int i, int source)
{
if (i < 0) {
return;
}
printPath(prev, prev[i], source);
if (i != source) {
cout << ", ";
}
cout << i;
}
// Comparison object to be used to order the heap
struct comp
{
bool operator()(const Node &lhs, const Node &rhs) const {
return lhs.weight > rhs.weight;
}
};
// Run Dijkstra’s algorithm on the given graph
void findShortestPaths(Graph const &graph, int source, int n)
{
// create a min-heap and push source node having distance 0
priority_queue<Node, vector<Node>, comp> min_heap;
min_heap.push({source, 0});
// set initial distance from the source to `v` as infinity
vector<int> dist(n, INT_MAX);
// distance from the source to itself is zero
dist[source] = 0;
// boolean array to track vertices for which minimum
// cost is already found
vector<bool> done(n, false);
done[source] = true;
// stores predecessor of a vertex (to a print path)
vector<int> prev(n, -1);
// run till min-heap is empty
while (!min_heap.empty())
{
// Remove and return the best vertex
Node node = min_heap.top();
min_heap.pop();
// get the vertex number
int u = node.vertex;
// do for each neighbor `v` of `u`
for (auto i: graph.adjList[u])
{
int v = i.dest;
int weight = i.weight;
// Relaxation step
if (!done[v] && (dist[u] + weight) < dist[v])
{
dist[v] = dist[u] + weight;
prev[v] = u;
min_heap.push({v, dist[v]});
}
}
// mark vertex `u` as done so it will not get picked up again
done[u] = true;
}
for (int i = 0; i < n; i++)
{
if (i != source && dist[i] != INT_MAX)
{
cout << "Path (" << source << " —> " << i << "): Minimum cost = "
<< dist[i] << ", Route = [";
printPath(prev, i, source);
cout << "]" << endl;
}
}
}
int main()
{
// initialize edges as per the above diagram
// (u, v, w) represent edge from vertex `u` to vertex `v` having weight `w`
vector<Edge> edges =
{
{0, 1, 10}, {0, 4, 3}, {1, 2, 2}, {1, 4, 4}, {2, 3, 9},
{3, 2, 7}, {4, 1, 1}, {4, 2, 8}, {4, 3, 2}
};
// total number of nodes in the graph (labelled from 0 to 4)
int n = 5;
// construct graph
Graph graph(edges, n);
// run the Dijkstra’s algorithm from every node
for (int source = 0; source < n; source++) {
findShortestPaths(graph, source, n);
}
return 0;
}
Kết quả khi chạy chương trình:
Path (0 —> 1): Minimum cost = 4, Route = [0, 4, 1] Path (0 —> 2): Minimum cost = 6, Route = [0, 4, 1, 2] Path (0 —> 3): Minimum cost = 5, Route = [0, 4, 3] Path (0 —> 4): Minimum cost = 3, Route = [0, 4] Path (1 —> 2): Minimum cost = 2, Route = [1, 2] Path (1 —> 3): Minimum cost = 6, Route = [1, 4, 3] Path (1 —> 4): Minimum cost = 4, Route = [1, 4] Path (2 —> 3): Minimum cost = 9, Route = [2, 3] Path (3 —> 2): Minimum cost = 7, Route = [3, 2] Path (4 —> 1): Minimum cost = 1, Route = [4, 1] Path (4 —> 2): Minimum cost = 3, Route = [4, 1, 2] Path (4 —> 3): Minimum cost = 2, Route = [4, 3]
Độ phức tạp của thuật toán: O(E.log(V))
💥 Đọc thêm về thuật toán:
- Thuật toán tìm kiếm nhị phân – Binary Search Tree (BTS)
- Thuật toán đảo ngược chuỗi liên kết (Linked List)
- Thuật toán Quick Sort – Java Example
Đăng kí nhận sách dạy kiếm tiền từ ứng dụng di động
Bạn đã bao giờ tự hỏi Hà Đông kiếm tiền tỷ từ Flappy Bird như nào không? Bạn biết cách lập trình nhưng lại không biết làm sao để kiếm được tiền từ nó?
Hiện cuốn sách đang bán rất chạy trên Amazon với giá 9.99$. Bạn có muốn nhận cuốn sách này để học kiếm tiền không? Đăng kí để nhận miễn phí nhé
Bình luận. Cùng nhau thảo luận nhé!