Các thuật toán tìm ước chung lớn nhất trong Java

Nằm trong series học thuật toán – cấu trúc dữ liệu và giải thuật, chúng ta cùng nhau tìm hiểu các phương pháp để tìm ước chung lớn nhất, code được minh họa bằng Java.

Trước hết, chúng ta cùng nhau tìm hiểu lý thuyết trước đã nhé.

Định nghĩa ước chung lớn nhất

Trước khi hiểu ước chung lớn nhất, bạn cần phải biết ước số là gì? Đơn giản lắm, ước số của một số nguyên a là số nguyên b khi và chỉ khi số a chia hết cho số b.

Ước chung lớn nhất (GCD – Greatest Common Divisor) của hai hay nhiều số nguyên là số lớn nhất trong tập hợp ước chung.

Ngược với ước chung lớn nhất là bội số chung nhỏ nhất. Mình sẽ dành riêng bài viết sau để hướng dẫn sử dụng thuật toán để tìm bội số chung nhỏ nhất. Các bạn đón đọc nhé.

Ứng dụng thực tế của ước chung lớn nhất (UCLN)

Với nhiều ứng dụng thực tế, ước chung lớn nhất không chỉ dùng trong lĩnh vực toán học, mà cả các lĩnh vực khác nữa, liên quan đến nhiều sự vật, hiện tượng trong đời sống.

Mình lấy ví dụ minh họa nhé:

Tôi chán làm dev, bỏ về quê chăn thỏ làm giàu. Đố bạn biết tôi đang nuôi bao nhiêu con thỏ? Dữ liệu cho bạn đây: Hàng này tôi luôn bỏ ra 6 cây súp lơ, 8 củ cà rốt làm thức ăn cho chúng. Mỗi con thỏ đều được thưởng thức cả súp lơ và cà rốt. Trong đó, số lượng súp lơ và cà rốt ăn được phải bằng nhau. Tất nhiên, không được bỏ thừa bất kỳ đồ ăn nào cả. Thế mới khó chứ.

Với bài toán thực tế này, bạn chỉ cần sử dụng UCLN là giải được (Gợi ý đáp án: 2 con thỏ).

Các thuật toán tìm ước chung lớn nhất

Để minh họa cho thuật toán tìm UCLN, chúng ta sẽ sử dụng ngôn ngữ Java cho quen thuộc.

Dưới đây là một số thuật toán tìm UCLN.

#1 – Sử dụng thuật toán vét cạn

Trong các thuật toán, có lẽ thuật toán vét cạn là thuật toán “nông dân” nhất, thủ công nhất. Mọi người hay đùa nhau, thuật toán vét cạn là thuật toán cứ tay to là thắng, khỏi cần suy nghĩ gì cả, kiểu “cần cù bù siêng năng”.

Với bài toán này, giả sử tìm UCLN của hai số nguyên (a, b). chúng ta sẽ tiến hành lặp từ 1 tới số nhỏ hơn trong hai số (a,b) và kiểm tra xem các số nguyên (a, b) có chia hết cho chỉ số index không? Chỉ số lớn nhất mà (a,b) chia hết chính là UCLN.

Cài đặt thuật toán bằng Java.

public static int gcdByBruteForce(int a, int b) {
        int gcd = 1;
        for (int i = 1; i <= a && i <= b; i++) {
            if (a % i == 0 && b % i == 0) {
                gcd = i;
            }
        }
}

Độ phức tạp của thuật toán là: O(min(a, b))

#2 – Tìm UCLN sử dụng thuật toán Euclid

Tìm UCLN của hai số nguyên (X,Y), giả sử x > y. Để tìm UCLN, chúng ta tiến hành chia x cho y, được phần nguyên a và số dư b (b>= 0). Ta có sơ đồ cho thuật toán Euclid như sau:

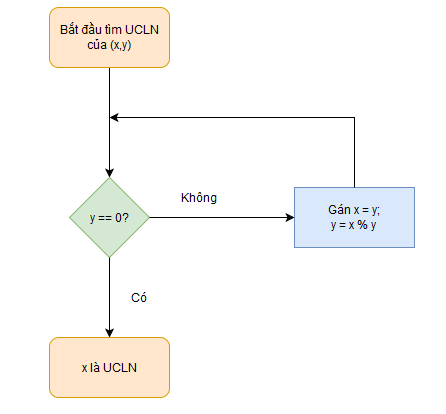
Cài đặt giải thuật bằng Java theo cách đệ quy.

    /*
     * Java method to find GCD of two number using Euclid's method
     * @return GDC of two numbers in Java
     */
    private static int findGCD(int x, int y) {
        //base case
        if(y== 0){
            return x;
        }
        return findGCD(y, x%y);
    }

Nếu bạn không thích đệ quy, có thể dùng vòng lặp while như sau:

// Code from https://vntalking.com
public static int findGCD(int x, int y) {
    int temp;
    while(y!= 0) {
        temp = x % y;
        x= y;
        y= temp;
    }
    return x;
}

Độ phức tạp thuật toán: O(Log min(x, y))

#3 – Thuật toán Stein (Binary GCD)

Cuối cùng, mình muốn giới thiệu thêm thuật toán stein hay còn gọi là thuật toán Binary GCD để tìm ước chung lớn nhất của hai số nguyên dương.

Thuật toán này sử dụng phép toán số học đơn giản như dịch số, so sánh và phép trừ.

Các bước của thuật toán:

• gcd(0, 0) = 0, gcd(n1, 0) = n1, gcd(0, n2) = n2
• Khi cả n1 và n2 đều là số nguyên chẵn thì gcd(n1, n2) = 2 * gcd(n1/2, n2/2) vì số chẵn luôn chia hết cho 2.
• Nếu n1 là số nguyên chẵn, còn n2 là số lẻ thì gcd(n1, n2) = gcd(n1/2, n2)
• Nếu cả n1 và n2 là số lẻ, và n1 >= n2 thì gcd(n1, n2) = gcd((n1-n2)/2, n2).

Sau đây là cài đặt thuật toán bằng Java.

public static int gcdBySteinsAlgorithm(int n1, int n2) {
        if (n1 == 0) {
            return n2;
        }

        if (n2 == 0) {
            return n1;
        }

        int n;
        for (n = 0; ((n1 | n2) & 1) == 0; n++) {
            n1 >>= 1;
            n2 >>= 1;
        }

        while ((n1 & 1) == 0) {
            n1 >>= 1;
        }

        do {
            while ((n2 & 1) == 0) {
                n2 >>= 1;
            }

            if (n1 > n2) {
                int temp = n1;
                n1 = n2;
                n2 = temp;
            }
            n2 = (n2 - n1);
        } while (n2 != 0);

        return n1 << n;
    }

Độ phức tạp thuật toán: O((log₂n1)²) hoặc O((log₂n2)²) tùy vào n1> n2 hay ngược lại.

Lời kết

Trên đây, mình đã giới thiệu 3 thuật toán phổ biến nhất để tìm UCLN của hai số nguyên. Trong đó, mình có minh họa bằng Java, nếu bạn thích C++ thì để lại comment bên dưới để mình chuyển sang C++ nhé.

Những thuật toán trên cũng rất hay được sử dụng trong các bài toán tìm kiếm. Rất mong bài viết này hữu ích với bạn!

🔥 Đọc thêm:

• 5 thuật toán mà mọi lập trình viên nên biết
• Tổng hợp series học lập trình chọn lọc

​Miễn phí khóa học React Native

Bạn có muốn download toàn bộ video của khóa học rất nổi tiếng về React Native này không? Đăng kí để mình gửi link download nhé

DOWNLOAD