Đệ Quy trong JavaScript: Hiểu Khái Niệm và Cách Ứng Dụng

Trong thế giới lập trình, có rất nhiều khái niệm thú vị và hữu ích mà bất kỳ lập trình viên nào cũng nên nắm rõ. Một trong số đó chính là đệ quy – một khái niệm vô cùng mạnh mẽ và linh hoạt, đặc biệt trong ngôn ngữ lập trình như JavaScript. Vậy, đệ quy là gì, tại sao nó lại quan trọng và làm thế nào để bạn có thể ứng dụng nó trong công việc của mình? Hãy cùng VNTALKING khám phá nhé

Tại sao lại là Đệ Quy?

Đệ quy, theo định nghĩa đơn giản nhất, là một phương pháp mà trong đó một hàm gọi chính nó để giải quyết một bài toán. Điều này nghe có vẻ hơi kỳ quặc, nhưng thực tế nó lại cực kỳ mạnh mẽ. Đệ quy cho phép chúng ta giải quyết những vấn đề phức tạp một cách dễ dàng hơn thông qua việc chia nhỏ vấn đề thành các phần nhỏ hơn và giải quyết từng phần một.

Ví dụ thực tế

Trước khi đi sâu vào lý thuyết, hãy cùng nhìn một vài ví dụ để thấy được sự hữu ích của đệ quy:

1. Tính giai thừa: Một trong những ứng dụng phổ biến nhất của đệ quy là tính giai thừa của một số. Bạn có thể tính giai thừa của 5 (5!) bằng cách nhân 5 với giai thừa của 4 (4!).
2. Duyệt cây: Trong cấu trúc dữ liệu cây, bạn có thể sử dụng đệ quy để duyệt qua các nút của cây một cách dễ dàng.
3. Giải quyết bài toán Fibonacci: Một trong những bài toán nổi tiếng có thể được giải quyết bằng đệ quy là tìm số Fibonacci.

Với những ứng dụng thực tế này, chúng ta có thể thấy rằng đệ quy không chỉ đơn thuần là một khái niệm lý thuyết mà còn có thể được ứng dụng rộng rãi trong thực tiễn.

Khái Niệm Đệ Quy

Đệ Quy Cơ Bản

Khi một hàm gọi chính nó, có hai phần chính trong hàm đệ quy:

1. Điều kiện dừng: Đây là điều kiện để ngăn hàm tiếp tục gọi chính nó vô hạn. Nếu không có điều kiện dừng, hàm sẽ tiếp tục gọi chính nó mãi mãi và dẫn đến lỗi tràn ngăn xếp (stack overflow).
2. Tình huống tái diễn: Đây là phần mã mà hàm sẽ gọi chính nó để xử lý phần còn lại của bài toán.

Ví dụ Đệ Quy Cơ Bản

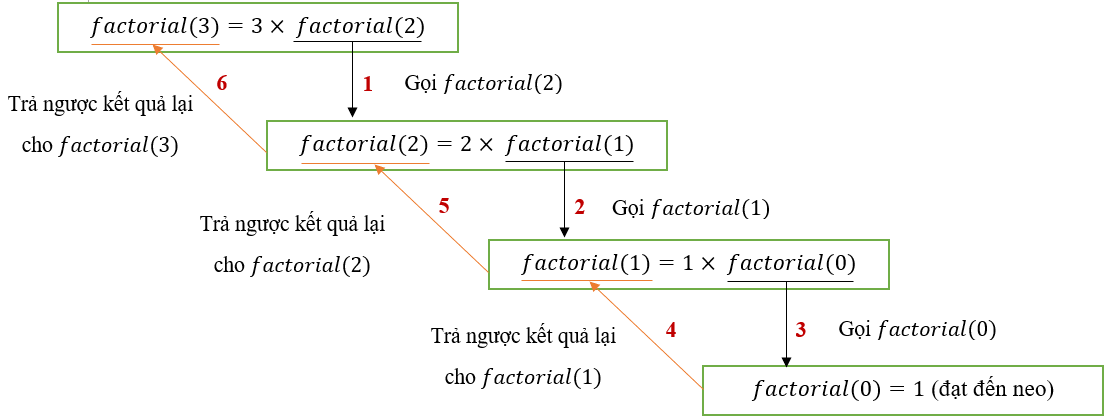
Hãy cùng xem một ví dụ đơn giản về tính giai thừa của một số:

function factorial(n) {
  // Điều kiện dừng
  if (n === 0) {
    return 1;
  }
  // Tình huống tái diễn
  return n * factorial(n - 1);
}

console.log(factorial(5)); // Kết quả: 120

Giải thích mã:

• Khi n bằng 0, hàm trả về 1, vì giai thừa của 0 là 1.
• Nếu n lớn hơn 0, hàm sẽ gọi chính nó với giá trị n - 1.

Ứng Dụng Đệ Quy

1. Duyệt Cấu Trúc Dữ Liệu

Đệ quy rất hữu ích trong việc duyệt qua cấu trúc dữ liệu phức tạp như cây và đồ thị. Dưới đây là một ví dụ về cách duyệt cây nhị phân:

class Node {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

function traverseTree(node) {
  if (node) {
    console.log(node.value); // Xử lý nút hiện tại
    traverseTree(node.left);  // Duyệt bên trái
    traverseTree(node.right); // Duyệt bên phải
  }
}

// Tạo cây ví dụ
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);

traverseTree(root);

Giải thích mã:

• Hàm traverseTree kiểm tra xem nút hiện tại có tồn tại hay không. Nếu có, nó sẽ in giá trị của nút và sau đó gọi chính nó cho các nút con bên trái và bên phải.

2. Giải Quyết Bài Toán Fibonacci

Bài toán Fibonacci có thể được giải quyết bằng đệ quy như sau:

function fibonacci(n) {
  if (n <= 1) {
    return n;
  }
  return fibonacci(n - 1) + fibonacci(n - 2);
}

console.log(fibonacci(6)); // Kết quả: 8

Giải thích mã:

• Hàm kiểm tra nếu n là 0 hoặc 1 và trả về giá trị tương ứng. Nếu không, hàm sẽ gọi chính nó hai lần để tính tổng hai số Fibonacci trước đó.

Kết Luận

Đệ quy là một khái niệm mạnh mẽ trong JavaScript mà mọi lập trình viên nên biết. Bằng cách chia nhỏ các bài toán phức tạp, chúng ta có thể sử dụng đệ quy để giải quyết các vấn đề trong lập trình một cách hiệu quả. Hy vọng qua bài viết này, bạn đã có cái nhìn rõ hơn về đệ quy và cách ứng dụng nó trong JavaScript.

Đừng ngần ngại thử nghiệm với mã code mà chúng ta đã thảo luận, và hãy để VNTALKING đồng hành cùng bạn trong hành trình học hỏi lập trình. Nếu bạn muốn tìm hiểu thêm, hãy tham khảo các tài nguyên bổ sung hoặc tài liệu học tập liên quan đến đệ quy và các khái niệm lập trình khác trên blog của mình.